Dr. Gerhard Paulus presenting an invited talk on "Applications with attosecond pulses" at Photonics West 2007
|
|
|
|
|
Dr. Gerhard Paulus uses specially mounted Del Mar Photonics' MCP-MA34/2 detector
http://faculty.physics.tamu.edu/ggp/

|
Dr. Gerhard G. Paulus Associate Professor Department of Physics Texas A&M University College Station, TX 77843 email: ggp@mpq.mpg.de |
Sektion Physik Ludwig-Maximilians-Universität München 85748 Garching |
| 2002 | Habilitation (Dr. rer. nat. habil.) |
| Ludwig-Maximilians-Universität München | |
| Max-Planck Institut für Quantenoptik, Garching | |
| 1995 | Dissertation (Dr. rer. nat.) |
| Ludwig-Maximilians-Universität München | |
| Max-Planck Institut für Quantenoptik, Garching | |
| (Prof. Dr. Dr. h.c. mult. H. Walther) | |
| 1992 | Diplom (Dipl. Phys.) |
| Ludwig-Maximilians-Universität München | |
| Max-Planck Institut für Quantenoptik, Garching | |
| (Prof. Dr. Dr. h.c. mult. H. Walther) |
NEW: Attosecond double-slit
experiment
| Generation of laser pulses with ever shorter duration made possible to obtain higher and higher intensities. Meanwhile, pulses of 10 fs duration and less can be produced, 1 Femtosecond being the billionth of a millionth of a second (10^-15s). Assuming a pulse energy of 10 mJ, this gives rise to a power of 10^12 W. Thus, for a very brief moment, such a laser is capable to deliver the power of hundreds of nuclear power plants. Numerous other impressive comparisons are possible. The pulses can be focused down to a spot size with a diameter comparable to the wavelength thus causing intensities of the order of 10^20 W/cm^2. Such intensities are associated with tremendous field strengths. The electric part would have an amplitude of 20 TV/m, i.e. values exceeding by many orders of magnitude all other field strengths produced by man. In fact, such truly astronomical values are only anticipated in atmospheres of stars etc. |  |
| Femtosecond lasers therefore easily reach and exceed typical field strengths in atoms. Accordingly, the laser light no longer can be considered to be a small perturbation of the atom. As a consequence a bunch of new phenomena in atom physics were discovered since the advent of powerful ultrashort laser pulses. Many of them were so surprising because we are used to look at atomic phenomena in terms of perturbation theory. Photoionization is one of the elementary processes. For sufficiently high intensity, an atom may absorb much more photons than necessary for its ionization leading to correspondingly high photoelectron kinetic energies (above-threshold ionization, ATI). Particularly intriguing (and in strong contrast to expectations from perturbation theory) had been the discovery that the electron yield can be almost constant over an extended region of the kinetic energy spectrum. Due to the characteristic appearance, this high-energy structure in photoelectron spectra is called the plateau. | 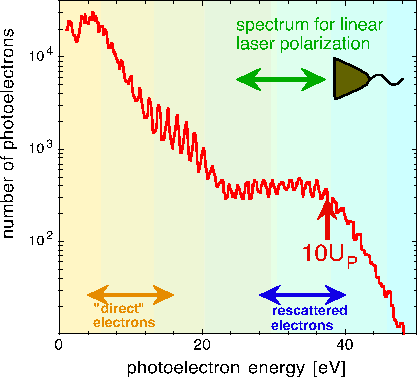 |
| Above-threshold ionization is certainly not the only interesting effect
of atoms in strong fields. Particular high attention has received the
generation of soft-X-ray radiation via harmonic generation of femtosecond
laser pulses. However, ATI, being a single atom effect, can be more easily
investigated. This as well as other considerations made ATI first choise to
investigate a new phenomenon appearing as laser pulse durations have been
reduced further to 5 fs. Such pulses consist (full-width half-maximum) of
less than two optical cycles only (few-cycle pulses). This means that the
pulse envelope changes almost as fast as the field oscillates. Therefore,
the temporal evolution of the field depends on the phase of the carrier wave
with respect to the envelope. This phase is commonly dubbed the absolute
phase because it determines a global feature of the pulse. A simple formula
helps to precisely describe what it is all about with the absolute phase of
a few-cycle pulse. For this we write the laser's electric field E(t) as a
product of the pulse envelope E0(t) and the carrier cos(ωt+φ):
E(t) = E0(t) cos(ωt+φ) . ω is the laser (circular) frequency which corresponds to an oscillation period of 2.6 fs at the common wavelength of 800 nm of current femtosecond lasers. Choosing the convention that t=0 at the maximum of the pulse envelope E0, an absolute phase φ=0 leads to "cosine-like" pulses (peak of the field at t=0), whereas φ=-π/2 leads to "sine-like" pulses (zero field strength at t=0). |
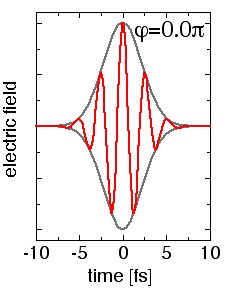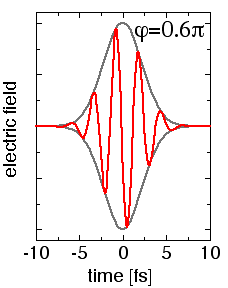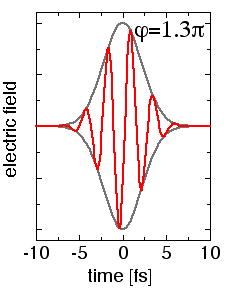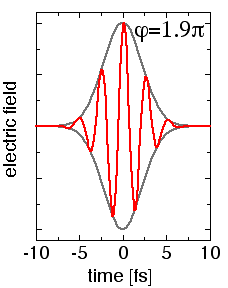 |
| For cosine-like pulses, the field is obviously stronger in positive
direction ("right") than in negative direction ("left"). One therefore
quickly asks oneself whether such a pulse couldn't pull out more electrons
to the right than to the left. This is indeed approximately true as our
group has shown in a series of experiments. The phase effects are particular
strong in the high-energy (plateau) part of the spectra.
Now one might adopt two different point of views: The phase-dependent
spectra can be considered as a measure of the absolute phase. Measuring the
absolute phase is an extremely important issue because the absolute phase
determines the temporal evolution of the electric field of the laser pulses.
The laser field in turn governs the manifold of phenomena which can be
induced. |
 |
Other possible applications are just too numerous to list and explain here —
besides the fact that the most interesting ones tend to appear as complete
surprises...
There is one application that already has taken great advantage of control of
the absolute phase: Generation of attosecond soft-X-ray pulses. Attosecond
science, i.e. science on the time-scale of electronic transitions and thus on
the time-scale of elementary chemical reactions, is an emerging field. Phase
control via ATI appears to be a key-technology for this field. However, our
experiments can also be interpreted as analysis of the most fundamental
electronic transition — namely photoionization — on the sub-100as scale.
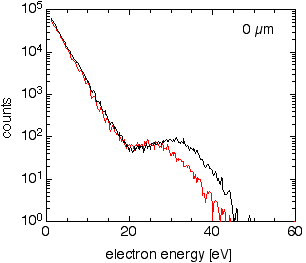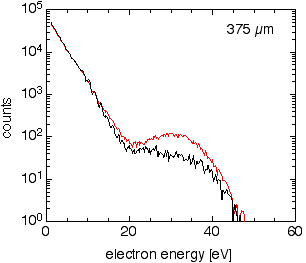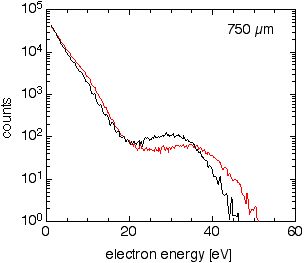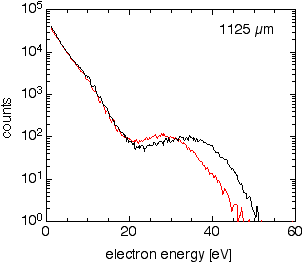
| Did I say that the most interesting developments tend to appear as surprises? Here is one: A few-cycle laser pulse can act as a single- or double-slit or anything in between. A close look at the movie above reveals that there is some peak structure in the spectra, particularly pronounced for energies between 10 and 20eV. Before dismissing them as weak or negligible, one should note that these spectra are plotted on a logarithmic scale. On the right there is a figure showing another measurement on a linear scale with some background subtraction. The spectra are shown for +/- sine-like pulses for both directions, and for all absolute phases in a false-color representation. The right panel of the false-color figure was recorded with the right detector and the left panel with the left detector. Accordingly, both panels show the same thing shifted by π. Someone familiar with ATI might say that these are just ATI-peaks. This is certainly not entirely wrong, but it is certainly not the complete story: Why does the contrast of the peaks and their position depend on phase? | 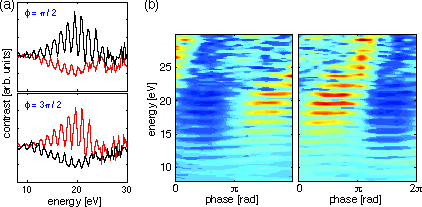 |
| Here is a better explanation: The peaks should be considered to be a
fringe pattern generated by a double-slit! For Young's double slit the
spatial geometry of the slits determines the fringes on the screen that are
measured in momentum space (the spatial coordinate becomes a momentum
coordinate after Fourier transformation). The fringes in this experiment are
recorded in the energy domain. The Fourier theorem then says that our slits
are temporal slits or windows in time. How this? Photoionization under the
present conditions is a very nonlinear process: A slightly lower field
results in a dramatic decrease of ionization probability. Now we can
understand, how a few-cycle laser pulse produces single- and double-slits:
Only close to the peaks of the field is there an appreciable probability for
ionization: The peaks of the field open the windows in time at which an
electron might be released by the atom. For a given direction there are — depending on the absolute phase — one or two equally strong peaks of the field or anything in between. If there is one temporal slit, we know of course exactly, at which time the electron was released. This is a single slit with complete which-way information: no interference. If there are two equally strong peaks in a given direction, then there are two temporal windows the electron can use. There is no which-way information and we have a double slit with a perfect interference pattern. A strong and a weak peak would be roughly compared to a double slit with a narrow and a broader slit. This corresponds to partial which-way information and a low-contrast fringe pattern. There is even the possibility that there is one peak of the field in one direction and two peaks in the opposite. We then have a single- and a double-slit at the same time! Another really neat feature is that the number and strength of the slits can be controlled by adjusting the delicate feature of few-cycle pulses discussed above: the absolute phase. The explanation given above is simplified insofar, as the electrons are deflected after their release by the oscillating electric field and the atomic potential. A more rigorous explanation can be found in a recent article published in Physical Review Letters. Another reference is a report by Peter Rodgers in the March issue of PhysicsWorld and PhysicsWeb . |
 |